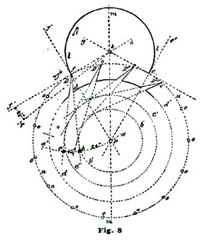
To "lay out" or delineate our escape-wheel teeth, we continue our drawing shown at Fig. 6, and reproduce this cut very nearly at Fig. 8. With our dividers set at five inches, we sweep the short arc a a' from f as a center. It is to be borne in mind that at the point f is located the extreme point of an escape-wheel tooth. On the arc a a we lay off from p twenty-four degrees, and establish the point b; at twelve degrees beyond b we establish the point c. From f we draw the lines f b and f c; these lines establishing the form and thickness of the tooth D. To get the length of the tooth, we take in our dividers one-half a tooth space, and on the radial line p f establish the point d and draw circle d' d'.

To facilitate the drawing of the other teeth, we draw the circles d' c', to which the lines f b and f c are tangent, as shown. We divide the circle n n, representing the periphery of our escape wheel, into fifteen spaces, to represent teeth, commencing at f and continued as shown at o o until the entire wheel is divided. We only show four teeth complete, but the same methods as produced these will produce them all. To briefly recapitulate the instructions for drawing the teeth for the ratchet-tooth lever escapement: We draw the face of the teeth at an angle of twenty-four degrees to a radial line; the back of the tooth at an angle of thirty-six degrees to the same radial line; and make teeth half a tooth-space deep or long.

We now come to the consideration of the pallets and how to delineate them. To this we shall add a careful analysis of their action. Let us, before proceeding further, "think a little" over some of the factors involved. To aid in this thinking or reasoning on the matter, let us draw the heavy arc l extending from a little inside of the circle n at f to the circle n at e. If now we imagine our escape wheel to be pressed forward in the direction of the arrow j, the tooth D would press on the arc l and be held. If, however, we should revolve the arc l on the center k in the direction of the arrow i, the tooth D would escape from the edge of l and the tooth D'' would pass through an arc (reckoning from the center p) of twelve degrees, and be arrested by the inside of the arc l at e. If we now should reverse the motion and turn the arc l backward, the tooth at e would, in turn, be released and the tooth following after D (but not shown) would engage l at f. By supplying motive to revolve the escape wheel (E) represented by the circle n, and causing the arc l to oscillate back and forth in exact intervals of time, we should have, in effect, a perfect escapement. To accomplish automatically such oscillations is the problem we have now on hand.